1.4.3 Apuntes para la desigualdad. e Revista JOOMAG

1.4.2 Desigualdad lineal

1.4.1 Desigualdades.

Una condición en x es una expresión que contiene la variable x y se transforma en una proposición matemática, es decir en una afirmación que es verdadera o falsa, cuando se sustituye x por un elemento del dominio en consideración, en nuestro caso por un número real. El conjunto de elementos del dominio que hacen de la condición una proposición verdadera, se llama el conjunto solución de la condición. La mayoría de las condiciones que se presentan en matemáticas tienen la forma de una ecuación o de una desigualdad. En esta sección estudiaremos algunas desigualdades y sus soluciones. Resolver una desigualdad es encontrar su conjunto solución, es decir encontrar todos los números reales que la hacen verdadera. El procedimiento para resolver desigualdades consiste en transformarlas en desigualdades equivalentes, es decir desigualdades que tienen las mismas soluciones, hasta que el conjunto solución sea obvio.

1.4 Desigualdades e intervalos.

La investigación de las cantidades numéricas implica comparar unas con otras o fijar la atención en un grupo determinado de números, por lo que estudiaremos ahora las desigualdades y los intervalos, herramientas fundamentales en la aplicación del cálculo.

1.3.3 Límites e Revista JOOMAG

1.3.2 Sistema de coordenadas rectangulares.

No siempre los fenómenos naturales o actividades realizadas se pueden presentar en un sistema de coordenada lineal, por lo que se propone el sistema de coordenada rectangular, también conocida como sistema de coordenadas cartesianas, que consiste en dos rectas perpendiculares. En la recta horizontal se presentan los valores del conjunto X, llamado eje de las x o eje de las abscisas, y en la recta vertical se representan los elementos de Y, el eje de las ordenadas o eje de las y. El punto donde se cruzan las dos rectas se llama origen del plano y se representa con la letra O. A la derecha y arriba del origen se disponen los valores positivos, y a la izquierda y abajo, los negativos. Cada una de las cuatro partes en que se divide el sistema de coordenadas se llaman cuadrantes y se enumeran en sentido contrario na las manecillas del reloj.

1.3.1 Sistema de coordenadas lineales.

Los fenómenos observados en la naturaleza, las actividades que realizas pueden ser representadas, en ocasiones, en una recta numérica, como la temperatura, la cuenta de ahorro, las ventas realizadas, etc. pueden ser representados en una recta numérica.
Esta gráfica se conoce como el sistema de coordenadas lineales.

1.3 Sistema de coordenadas lineales y rectangulares.

Una gran cantidad de actividades en los seres vivos, en los fenómenos de la naturaleza, se pueden representar en forma gráfica mediante un sistema de coordenadas lineales o rectangulares.

1. Introducción.

Los materiales que a continuación se te brindan tiene la intención de conducirte en el aprendizaje del Cálculo, realiza las actividades propuestas, apoya con los libros de texto, documentos en páginas de consultadas en la WEB, las participaciones con grupos o equipos de trabajo.
Esperando que la modalidad te sea útil y de beneficio te deseo éxito en tu trabajo educativo.

1.2.2 Producto cartesiano de dos conjuntos.

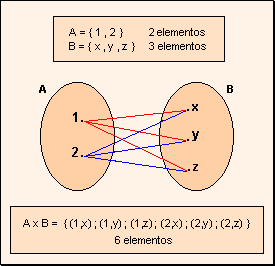
El producto cartesiano se puede representar por medio de una tabla, diagrama de flechas, diagrama de árbol, gráfico cartesiano o par ordenado.
El producto cartesiano de X por Y es el conjunto de todos los pares ordenados que se pueden formar con un elemento perteneciente al conjunto X y un elemento del conjunto Y, en los que el primer elemento pertenece a X y el segundo elemento a Y.

1.2.1 Conjunto de números.

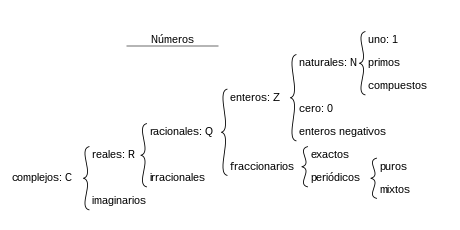
Los números reales son todos los números irracionales y racionales (enteros y naturales), como por ejemplo: 6, 35, -12, 3.5. El conjunto de números reales representado por ( R ), contiene a los subconjuntos de números irracionales ( I ) y a los racionales ( Q ); estos últimos contienen al subconjunto de números enteros ( Z ) y éste a su vez contiene al subconjunto de números naturales (N). Los números imaginarios se obtienen al presentarse la situación de querer obtener la raíz cuadrada de un número negativo.

Realiza el concepto de cada concepto:

1. Número real.
2. Número irracional.
3. Número racional.
4. Número entero.
5. Número natural.
6. Número imaginario.

1.2 Los números reales y sus operaciones.

Un número es la expresión simbólica de una cantidad asociada generalmente con objetos. El término "número" proviene del latín numerus que hace referencia a un signo o un conjunto de signos.

Clasificación de los números.

1.1 Antecedentes históricos.

Los personajes que hicieron aportaciones importantes al conocimiento que da bases al cálculo infinitesimal son: Nicolás Oresme, Johannes Kepler, Pierre de Fermath, Isaac Barrow, Isaac Newton, Gottfried Wilhelm von Leibniz, Leonhard Paul Euler,, Simon Antoine Jean L'Huiller y Agustín Louis Cauchy.
Los estudios sirvieron para comprender el estudio en el movimiento de los cuerpos, estudiando y aplicando el cálculo diferencial y el cálculo integral.
Investiga por equipo la biografía de uno de los personajes para exponer su trabajo realizado.